Kepler's Laws


Kepler's Laws
1. Orbits are conic sections with the force center at the focus.	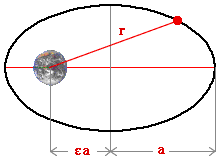Kepler's Laws of orbital mechanics were published in 1618 by Johannes Kepler who deduced them from reams of astronomical data. Kepler's Laws follow mathematically from Newton's Laws of motion and from his formula for the gravitational force. Conic sections are mathematical curves that include the circle, the ellipse, the hyperbola and the parabola. They are called conic sections because they can be obtained by slicing through a cone.
2. The satellite moves around an orbit in such a way that the radius vector sweeps equal areas in equal times.	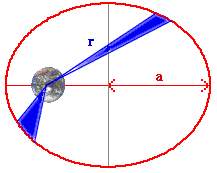This law is a mathematical consequence of conservation of angular momentum mv x r. The satellite moves faster when it is closer to the focal point of the orbit. The satellite's total energy, which remains constant, is divided between the kinetic energy and the potential energy.
3. Kepler's third law relates the period of satellite motion to the size of the orbit.	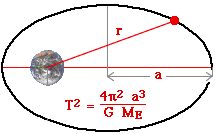For a circular orbit this law can be derived mathematically by setting the gravitational force on the satellite equal to the centripetal force.