|
 |
 |

Home
 "What is
Physics Good For?"
"What is
Physics Good For?"
Extra credit is available at the end of this page. Please respond before 9 AM, Monday, March 26th, 2001.
One of the most beautiful of all natural phenomena is the rainbow. For many of us in the sciences, fascination with the rainbow is among our earliest memories of curiosity about the natural world. Indeed, throughout history, people all over the world have by struck by the seemingly mystical quality of rainbows. Rainbows play important roles in the mythology of the  Norse, Navajo and other Native Americans,
the Gagudju people of Australia, and
many other cultures. In addition to
appreciating the beauty of a rainbow, we can also
understand it using what we have learned. The
picture to the left is a painting of a rainbow by a
3 year old child. Notice the pattern of colors (red
outside, blue inside) is this the pattern in a
natural rainbow? We will see that it is, and why,
we will also learn about the width of the rainbow,
the size of the arc, and where the rainbow appears
in the sky. Norse, Navajo and other Native Americans,
the Gagudju people of Australia, and
many other cultures. In addition to
appreciating the beauty of a rainbow, we can also
understand it using what we have learned. The
picture to the left is a painting of a rainbow by a
3 year old child. Notice the pattern of colors (red
outside, blue inside) is this the pattern in a
natural rainbow? We will see that it is, and why,
we will also learn about the width of the rainbow,
the size of the arc, and where the rainbow appears
in the sky.
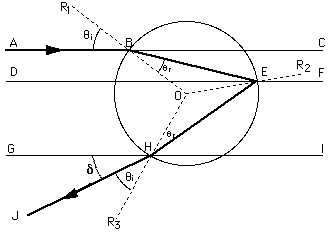
The rainbow is created by refraction and reflection of sunlight by water droplets. The geometry is more complicated than that of a prism, but nothing we can't handle. By considering how a few beams of light interact with an idealized spherical raindrop, we will determine a few basic facts about rainbows that you can go out and see for yourself. These are facts that you probably have already seen, but may not have really noticed. The following discussion all refers to the diagram below. Here are a few important geometerical facts: Lines ABC, DEF, and GHI are parallel. The dashed lines R1, R2, and R3 are radial, and thus are perpendicular to the surface of the drop at B, E, and H.
We consider a single ray of sunlight; it enters
the picture at point A and is refracted into the
drop at point B. The ray hits the back of the drop
at point E and is reflected to point H. There, it
is refracted out of the drop and leaves the picture
at point J. The ray is now traveling down towards
earth at angle delta.
First, notice that the triangles OBE and OEH are congruent (identical), isoceles triangles. We know this because angles BEO and OEH are the same (theta incident = theta reflected), and because line segments OE, OB and OH are all the same length. This means that angles OBE, OEB, OEH, and OHE are all the same. To get an expression for delta, we start at B and keep track of the angle of the ray with respect to the horizontal at each point:
That's the end of step one. Now, use Snell's law, nasin(theta
a)=nbsin(theta b). In this case,
na=1 theta a=theta i and theta b=theta
r. so sin(theta r)=sin(theta i)/nwater.
We get 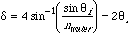
That's the end of step 2. Now, let's make a quick table of values of theta i, theta r, and delta.
It looks like delta has a maximum near theta i = 60. In fact, we can write an explicit formula for delta and take its derivative, set the derivative=0 and solve to find the maximum. This is step 3. 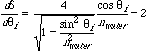
Using the expression obtained (an extra credit problem!) we find that for n=nred delta is a maximum for theta i=59.41 degrees. For n=nviolet=1.346, delta is a maximum for theta i=58.66 degrees. Plugging these values back into the equation for delta, we find that the maximum delta is 42.08 degrees for red light, and 40.22 degrees for violet light. This completes step 4. Now for step 5, the conclusion. Imagine yourself standing with the sun at your back, exactly 20 degrees above the horizon. You are looking up at a bunch of raindrops at various angles above the horizon in front of you. For red light, the maximum delta is 42.08, so looking 42.08-20 = 22.08 degrees above the horizon, you can see only red refracted light. As you look lower down, there will still be red light, but new colors will be added one at a time: first orange, then yellow, green, etc. As each color is added, your eye perceives the series as a series of colors. When you are looking at an angle of 40.22-20 = 20.22 degrees above the horizon, the violet light will be added. The whole process takes 22.08-20.22 = 1.86 degrees. This would be the angular width of the rainbow if the sun were really a single point in the sky. Actually the sun is about 1/2 degree wide itself, so the rainbow is about 2.36 degrees wide. A few notable features of this analysis of the rainbow:

You can get a lot more information about this subject on the internet. Here are a few search enginesAnd here are a few good links to get you started. 1.   
This site is made possible by funding from the National Science Foundation (DUE-9981111). |