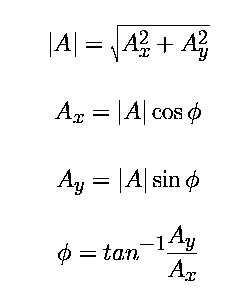Scalars and Vectors
Scalars and Vectors
Mathematics is the language of physics. With it, we can quantitatively describe
the world around us. In mechanics, we will use two types of quantities to
represent concepts like force, mass and time numerically. These two types
are known as scalars and vectors.
Goals
- Learn the definitions of scalars and vectors.
- See some examples of vector and scalar quantities.
- Translate vectors to and from their components.
- Understand how to add, subtract and multiply vectors.
Definitions
Scalar:
Scalars are used to describe one dimensional quantities,
that is, quantities which require only one number to completely describe
them. Examples of scalar quantities are:
Temperature
Time
Speed
Mass
Location Along a Line (1D)
|
Vector:
Vectors are used to describe multi-dimensional
quantities. Multi-dimensional quantities are those which require more than
one number to completely describe them. Vectors, unlike scalars, have two
characteristics, magnitude and direction. Examples of vector quantities are:
Location in a Plane (2D)
Location in Space (3D)
Velocity
Acceleration
Force
|
Note:
The drawings on this page contain many vector diagrams. We
will use colors to distinguish what each vector represents. The table below
shows the color scheme that we will be using from now on.
| Vector Color |
Meaning |

|
Arbitrary Vectors
(Red)
|
|
Vectors in X Direction
(Blue)
|

|
Vectors in Y Direction
(Green)
|
|
Resultant Vectors
(Black)
|
|
Coordinate Axes
(Gray)
|
Vector Diagrams
We use vector diagrams to visualize what is going on in a physical system.
Even though we can work out most problems algebraically, a picture can help
point out subtleties of a problem. The first step when solving any problem
in physics is to draw a picture.
The following diagram illustrates two points. The first is the concept of
the tip and the tail of a vector. With vectors, direction is
very important so we put an arrowhead in the direction that the vector is
going. This is sometimes called the tip of a vector. The other end is
usually called the tail.
The second concept that the diagram shows is that two vectors with the
same magnitude and direction are the same. This allows us to move
vectors around the coordinate system to help simplify the math involved with
them.

Expressing Vectors Using Components
Vectors can be expressed in terms of their magnitude and direction or in
terms of their components. Being able to translate between the two
representations is an essential skill in physics. The magnitude of a vector is
its length. The direction is usually given in terms of some angle.
When dealing with vectors it is usually much more convenient to break them up
into component vectors. Component vectors are vectors which run parallel to the
coordinate axes. For instance, a two-dimensional vector has two component
vectors, one in the X direction, and one in the Y direction. The diagram below
shows a two dimensional vector and its components.

The length and components for vector A, and the angle Ø
("Phi") are computed as:
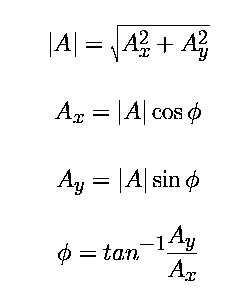
Vector Addition
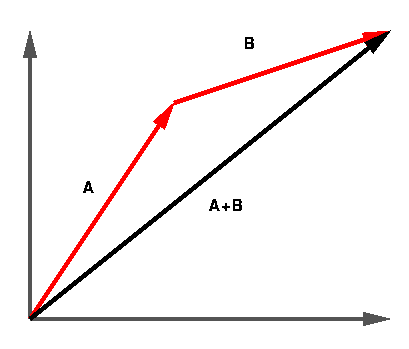
The following diagram illustrates a vector sum. Notice that we may move the
tail of the second vector to the tip of the first vector to get the resultant
vector. It does not matter which vector is moved, as long as the are
tip-to-tail with each other.
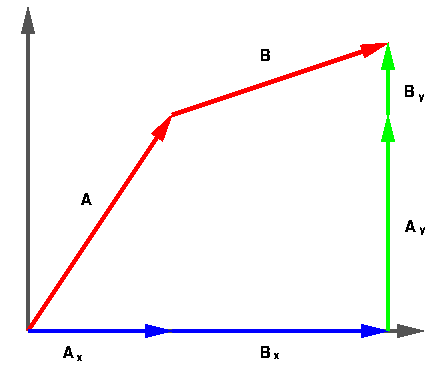
Once the vectors are expressed as their independent components, it is
possible to add them. Since each component is a scalar they may added
normally to the same component of the other vector. Conceptually, it looks
like the following diagram.
Multiplication of a Vector by a Scalar
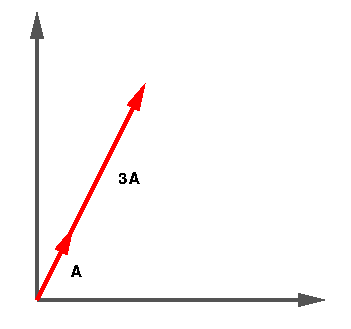
A vector may be multiplied by a scalar by multiplying each of its
components by that number. Notice that the vector does not change direction,
only length. If A = (1,2) then 3A = (3,6). This is shown
pictorially below.
A special case of vector multiplication is when we multiply a vector by
-1. This causes the vector to reverse direction. We will use this
property to perform vector subtraction.
Vector Subtraction
The vector difference works the same as vector addition except that we
multiply the vector we are subtracting by -1. It is much like
subtracting two numbers: A - B = A + (-B). The diagram below
illustrates vector subtraction in the tip-to-tail style. The original
B vector is shown as a dotted line.
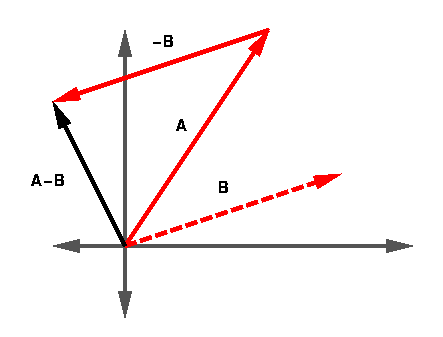
Remember that the order of the vectors being subtracted is important.
If you get them backward, the resultant will be in the opposite direction.
ie. A - B = -(B - A)
Example 1

A hiker walks 53.1 degrees north of east for 2.5km then due east for 2.0km.
What is her total displacement from her starting point if you measure the
distance along a straight line?
Example 2
A telephone pole support cable is in the way of some construction workers.
In order for the work to proceed, the cable must be moved 2 meters closer to
the pole. If the pole is 10 meters tall and the cable is currently fastened
to the ground 8 meters from the pole, how much will the workers need to
cut off from the cable when they move it?
Solutions